Last updated on: January 23, 2023
How to Calculate Deflection Angle and Measured with Accuracy
Measuring angles accurately is essential in surveying projects. A deflection angle is the angle between a survey line and an original course, and it can be used to locate points in different directions. Learn how to calculate deflection angle in surveying and make sure your project is done right with this guide. Also learn the definition, measurement and method of deflection angle and find out how to use a formula to calculate the deflection angle of the traverse for setting out a horizontal curve.
What is Deflection Angle?
The Deflection angle is the angle by which a line is deflected from its original direction.
In other words, It is the angle that a survey line makes with the extension of the proceeding line.
The direction may be towards the right or the left, depending upon whether the angle is measured clockwise or anticlockwise direction from the extension of the proceeding line.
Deflection angles are measured for designing horizontal curves in railways, highways etc
Importance of Deflection Angle:
The deflection angle is the angle between the tangents at the beginning and end of a curve. It is used in surveying and construction to determine the length and shape of a curve, and is typically measured in degrees.
The deflection angle is an important factor in setting out a circular curve, as it determines the necessary adjustments that need to be made in order to achieve the desired shape and length of the curve.
Deflection Angle Formula:
It is typically calculated using a formula such as:
L = (r*θ)/57.3
where L is the curve length, r is the radius of the curve, and θ is the deflection angle in radians.
The deflection angle is commonly used in the process of setting out horizontal curves in surveying and construction projects.
Methods of Calculating Deflection Angles in setting out Curve:
There are several methods of determining the horizontal curve deflection angle in surveying, including the following:
1- Chord method:
This method involves calculating the deflection angle using the length of the chord and the radius of the curve. The deflection angle is then calculated using the formula (deflection formula):
θ = 2arcsin(L/(2r))
where L is the chord length, r is the radius, and θ is the deflection angle in radians.
2- Deflection angle method:
This method involves calculating the deflection angle using the length of the curve and the radius of the curve. The deflection angle is then calculated using the deflection formula:
θ = (L*57.3)/r
where L is the curve length, r is the radius, and θ is the deflection angle in radians.
3- Middle ordinate method:
This method involves calculating the deflection angle using the middle ordinate of the curve and the radius of the curve. The deflection angle is then calculated using the formula:
θ = 2*arcsin (M/r)
where M is the middle ordinate, r is the radius, and θ is the deflection angle in radians.
4- Bearings method:
This method involves calculating the deflection angle using the bearings of the tangents at the beginning and end of the curve. The deflection angle is then calculated using the formula:
θ = (B2 – B1)/2
where B1 is the bearing of the first tangent and B2 is the bearing of the second tangent.
5- Tangent offset method:
This method involves calculating the deflection angle using the tangent offset of the curve and the radius of the curve. The deflection angle is then calculated using the formula:
θ = 2*arcsin (TO/r)
where TO is the tangent offset and r is the radius.
Measurement of Deflection Angle:
Theory:
The deflection angle refers to the angle formed between a survey line and the extension of the preceding line.
Instrument required:
Theodolite
Ranging rods
Steps for calculating deflection angle using Theodolite:
To measure a deflection angle using a theodolite, follow these steps:
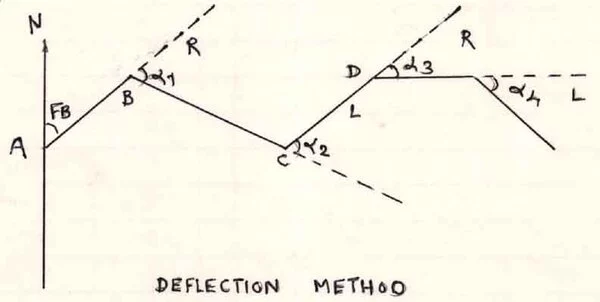
- Set up the theodolite at station A and measure the bearing of line AB.
- Set up the theodolite at station B and level it accurately.
- Set the vernier at station A to read 360 degrees or 0 degrees and read the vernier.
- Loosen the lower clamp and bisect station A accurately. Record the vernier readings.
- Transit the telescope.
- Release the upper plate and bisect station C using the upper tangent screw.
- Record the readings of both verniers. The mean of the two Vernier readings gives the value of the deflection angle at B.
- Loosen the lower plate and turn the telescope in a horizontal plane. Bisect station A again with the verniers still reading the same approximate value of the deflection angle and the telescope inverted.
- Transit the telescope and release the upper plate. Take a foresight on station C. Record the readings of both verniers.
- Calculate the mean of the final vernier readings, which gives twice the value of the deflection angle. One-half of this mean value will give the value of the deflection angle at B.
- Repeat the entire process to find the deflection angles at stations C, D, etc.
How to Measure Deflection Angle between two Points:

Tips for accurate Deflection Angle Measurement:
Here are some tips for accurately measuring a deflection angle using a theodolite:
1- Ensure that the theodolite is level and calibrated. An accurately levelled theodolite is essential for accurate deflection angle measurement.
2- Take multiple readings and average them. This will help to minimize errors and ensure the most accurate measurement.
3- Check for errors and make necessary adjustments. If the measurement is not consistent with the expected result, it is important to check for errors and make any necessary adjustments to ensure accuracy.
4- Use a transit or other surveying equipment to check the accuracy of the deflection angle measurement.
Follow the proper procedures and techniques for accurately measuring a deflection angle using a theodolite. This may include techniques such as bisecting the point of tangent intersection, transit the telescope, and releasing the upper plate.
Conclusion:
In conclusion, deflection angle is an important factor in surveying and construction projects, as it determines the shape and length of a simple curve. There are several methods available for calculating deflection angle, including the chord method, deflection angle method, middle ordinate method, bearings method, and tangent offset method.
Theodolites are commonly used to measure deflection angle, and it is important to ensure that the theodolite is level and calibrated before beginning the measurement. By following proper procedures and techniques, and by taking multiple readings and averaging them, it is possible to accurately measure deflection angle in simple curve and successfully set out a curve in surveying and construction projects.
OTHER POSTS:
-
Thumb Rules for Civil Engineering
-
Method Statement for Cast in Place Concrete Works
-
Method Statement for Bituminous Damp Proofing for Concrete and Masonry
-
Method Statement for Trench Excavation and Backfill for Electrical Cables
FAQs:
What is deflection angle in traverse?
The angle of deflection can be applied in an open traverser where traversers make small deflections such as railways, canals, sewer pipes etc.
Deflecting angle = 120°.
What is the difference between tangential angle and deflection angle?
Tangential angle is the angle between the tangent of a curve and a line perpendicular to the tangent, while deflection angle is the angle between the tangents at the beginning and end of a curve.
Can deflection angle be more than 90 degrees?
Deflection angles range from 90 degrees to 180 degrees, but can be used at values below 90 degrees. Deflection angle is the angle between the tangents at the beginning and end of a curve, and it can be any value depending on the shape of the curve. A curve with a deflection angle of more than 90 degrees would be a sharp curve, while a curve with a deflection angle of less than 90 degrees would be a more gradual curve.
What is deflection angle in traverse?
Traversed in Deflective Angle. The Deflective Angle is the angle at which the survey line is extended to the previous line. The right or left position is designated by measuring clockwise / anticlockwise in the direction the previous line extends or reverses.
What is the importance of deflection angle?
Deflection angle is crucial for setting out a curve accurately in survey and construction projects. Accurate measurement of the deflection angle ensures that the curve is correctly shaped and the necessary adjustments are made to achieve the desired curve.
How can I ensure accurate deflection angle measurement in surveying?
To ensure accurate deflection angle measurement in survey works, it is important to ensure that the theodolite or other survey equipment is level and calibrated. It is also important to take multiple readings and to average them to minimize errors. Checking for errors and making necessary adjustments can also help to ensure accuracy.
What is the angle of deflection?
The deflection angle is the angle between the upward extend of the preceding leg to the direction.





valued content
Thanks for comment, For more related posts please visit Civil, Arch, Electrical and Mechanical Tab in File menu